Le mouvement des planètes et des satellites pour les nuls

Bonjour jeune Homo-Sapiens, sais-tu que tu habites sur une planète ? Oui, bien sûr merci Captain Obvious mais sais-tu que celle-ci bouge ? Captain Obvious 2ème fois merci ! En clair, t'es-tu déjà demandé comment celle-ci se déplace, quelles sont les propriétés de son mouvement ? Car oui, une planète ou un satellite ne se déplace pas selon son bon vouloir, ils suivent des règles et je suis là pour te les expliquer ! Mais d'abord, retour vers le passé (Like si tu connais Code Lyoko). Et on commence tout de suite par une petite révision en vidéo pour le Bac.

Les lois de Kepler

En 1571 né Johannes Kepler, célèbre astronome et physicien que mes confrères de Terminale S doivent adorer. Après de longues études, car oui tu trouves pas des putains de propriétés célestes comme ça, Kepler démontra 3 lois en 1609 et 1618 : la loi des orbites, la loi des aires et la loi des périodes.

1er loi de Kepler : la loi des orbites

Bon alors à l'époque, on n'était pas totalement con, on savait déjà que la Terre était ronde, que le Soleil était le centre du système solaire et que les planètes tournaient autour (du moins celles que l'on connaissait), MAIS on pensait que ces trajectoires étaient des cercles parfaits. Et là Kepler met un High-Kick à l'astronomie de l'époque en démontrant la loi des orbites, qui dit que les planètes ne suivent pas des trajectoires circulaires mais des trajectoires elliptiques !

Chaque planète de notre système solaire décrit autour de notre Soleil une ellipse dont le Soleil est un des foyers, l'autre étant inoccupé.

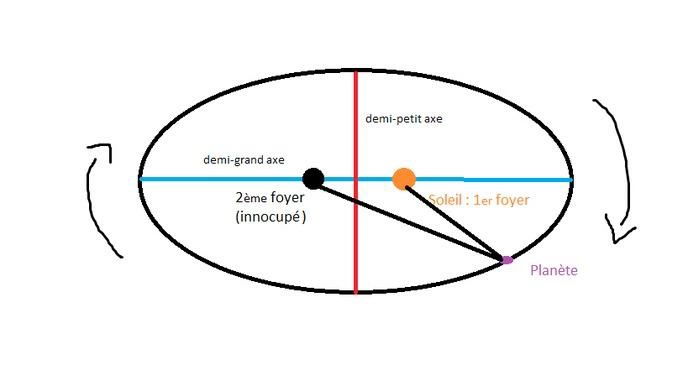
2e loi de Kepler : la loi des aires

Suite à cette découverte remarquable pour l'époque, Mr Kepler s'intéressa plus précisément à l'ellipse parcourue et donc aux distances et aux surfaces parcourues par une planète. Sur mon magnifique dessin Paint, paye ta crédibilité, on peut voir 4 points qui représentent une planète à des instants différents ainsi que le soleil. La loi dit que le rayon qui joint la planète au soleil balaye des surfaces égales pendant des durées égales.

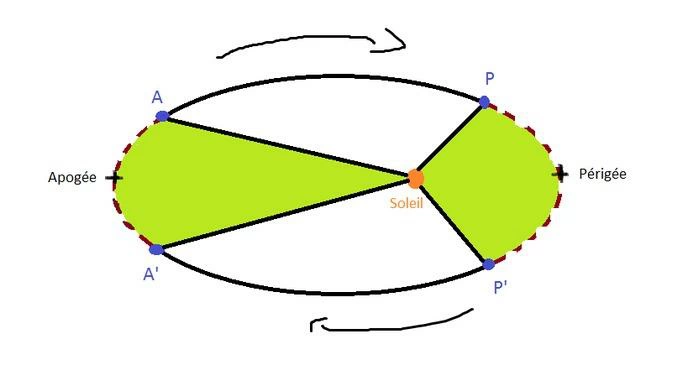
Pour vous représenter ça (le Soleil sera représenté par la lettre S) :
On pose SP, SP', SA, SA' des rayons
SPP' = aire balayée par la planète pendant une durée T
SAA' = aire balayée par la planète pendant une durée T'

Alors ici j'en appelle à votre logique scientifique, montrez moi que notre communauté est intelligente !
1 - Si T et T' sont égales, alors les aires sont égales.
2 - Si T et T' sont égales, alors l'aire de l'arc PP' est supérieur à l'aire de l'arc AA' forcément. Donc la vitesse entre P et P' est plus grande que celle entre A et A'.

Grâce à ses observations et résultats, on peut en déduire que la vitesse de la planète est plus élevée lorsque la planète se rapproche du Soleil et diminue lorsqu'elle s'en éloigne. Ce mouvement n'est donc pas uniforme car la planète atteint sa vitese maximale à la périgée et sa vitesse minimale à l'apogée.
De cette loi, on peut dire que la force exercée sur la planète est constamment dirigée vers le Soleil.

Pour vous donner un exemple concret de l'utilisation de cette loi, on a pu découvrir pourquoi les saisons présentaient des durées différentes, comme l'hiver qui dure 89 jours contre l'été avec 93 jours.

3e loi de Kepler : la loi des périodes

Et enfin la dernière loi, la plus attendue, la plus recherchée, celle qui permet de définir la trajectoire selon un ordre mathématique, la période de révolution d'une planète. ATTENTION : ne pas confondre période de révolution et période propre d'une planète. La période de révolution est le temps que met la planète pour parcourir l'ellipse autour du soleil, la période propre est le temps que met la planète pour faire une rotation complète autour d'un de ses axes (la Terre qui tourne sur elle-même).

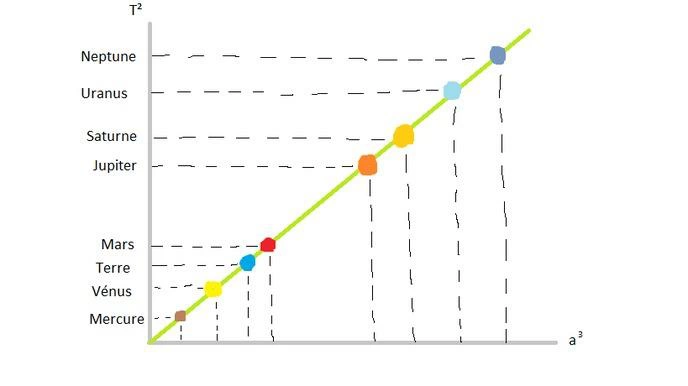
Je sais que la Terre a un demi-grand axe = 149597887,5 km (merci seigneur Wiki). On applique donc la formule de Kepler et on peut retrouver que la Terre a environ une période de révolution de 366 jours (bon je sais que c'est 365 jours, mais les données sont approximatives, vous allez pas râler).

Les applications sont donc nombreuses et ont considérablement fait avancer l'astronomie de l'époque, en permettant notamment d'émettre la certitude que les planètes les plus lointaines du soleil étaient les plus lentes.

La satellisation

"Ok c'est bien joli tes lois compliquées, mais c'est pas comme ça que je vais mettre quelque chose en orbite". Patience jeune pomme, voilà le savoir qui arrive.

La force principale qui relie un objet à la Terre est l'attraction terrestre, c'est simple : si tu sautes en l'air, tu vas retomber grâce à l'attraction terrestre. Pour mettre un satellite en orbite, et ainsi que vous puissiez avoir la TV et vous abrutir devant des émissions que je ne citerai pas, on l'embarque dans une fusée qui est lancée depuis le sol. Celle-ci utilise le moteur pour décoller, logique soit-dit en passant, on appelle ce phénomène la propulsion par réaction : le moteur va éjecter une quantité de gaz à très grande vitesse qui va créer une force de pousée capable de s'opposer à la force gravitationnelle de la Terre.

Petit exemple pour illustrer ce qu'est la force poussée, car oui je sais que vous raffolez de mes schémas !

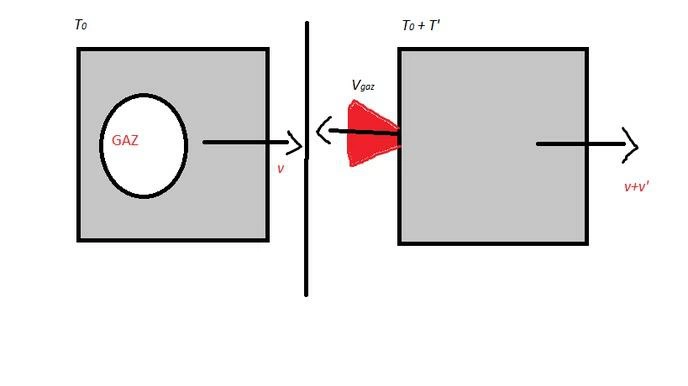
Imaginons une sonde loin de notre système solaire et éloignée de toute force gravitationnelle (sonde Voyager 1 et 2 en 1977). La sonde de masse M, de vitesse v à un instant t0 éjecte sur une durée T' une partie de sa masse sous forme de gaz à une vitesse Vgaz (comme quand tu flatules). La vitesse de la sonde à l'instant T+T' est égale à V+V'

Cette force de pousée est proportionnelle à la vitesse et aux débits massiques de gaz éjectés (comme quand tu flatules 2ème fois...). Fp = Dgaz x Vgaz. Voilà jusque ici votre fusée a décollé, a vaincu l'attraction terrestre si la force de pousée y est supérieure et s'apprête à lachêr son satellite. Mais comment faire pour que ce satellite soit bien fonctionnel et ne se casse pas la gueule sur la Terre ou ne se perde dans l'espace ?

Un satellite tourne autour d'un astre avec une vitesse constante. Contrairement à une idée répandue, le satellite n'est pas en apesanteur. Il est même en permanence en chute libre, mais, grâce à sa vitesse, il tombe "à côté" de la Terre. Sans le frottement de l'air, on pourrait satelliser à n'importe quelle altitude, en évitant les obstacles bien sûr. Mais l'atmosphère empêche de placer un satellite à moins de 200km d'altitude. Quelle planète contraignante. Le satellite placé aussi bas ne tiendra que quelques jours. Freiné par l'air, sa vitesse diminuera et il reviendra sur Terre. La vitesse à donner à un satellite diminue avec l'altitude de celui-ci. Plus il est haut, moins il est soumis à la gravité. La vitesse de satellisation est de 8 Km.s à 200km et 6,9 à 2000 km.

Voilà j'espère que cet article vous a plu, que vous en avez plus appris sur les mouvements dans l'espace, la mécanique céleste et que vous deviendrez tous de futurs ingénieurs spatiaux grâce à moi ! N'hésitez pas dans les commentaires à me poser des questions sur certains points que je n'ai pas explicité ou sur des questions que vous vous posez !

PS : pour les intéressés, voici quelques formules plûtot utiles :