Geekbusters : Batman est-il vraiment capable de voler ?

Après l'armure d'Iron Man, le marteau de Thor et le bouclier de Captain America, on va aujourd'hui se lancer dans l'univers DC Comics en se penchant sur le cas de Batman. Est-il vraiment capable de voler, comme nous le voyons dans les films et jeux vidéo ? Nous allons le voir tout de suite !

Une cape efficace pour voler

Dans les films Batman et The Dark Knight et dans les jeux vidéos Batman, nous pouvons voir que l'homme chauve-souris est capable de planer grâce à sa cape puis d’atterrir au sol sans aucun problème. Un bel exploit quand on sait que Bruce Wayne n'a aucun pouvoir. En effet, ce dernier ne dispose que d'une cape qui est fabriquée à partir d'un matériau intelligent qui peut se solidifier lorsqu'il est soumis à un champ électrique. Si ce dernier est capable de voler, ou plutôt de planer, est-il vraiment capable d'atterrir sans aucun dégât lorsqu'il saute du haut d'un building ?

3 forces agissent sur Batman

C'est ce à quoi ont répondu les étudiants D.A. Marshall, T.O. Hands, I. Griffiths, G. Douglas du département de Physique et d'Astronomie de l'université de Leicester et autant vous dire que le résultat va vous surprendre ! Pour cela, ils se sont intéressés au film Batman Begins où le héros saute d'un building haut de 150 mètres, aux différentes forces qui agissent sur le héros et à sa fameuse cape. Au total, il y a trois forces en présence, à savoir la traînée (D = 1/2 x C_D x ρ x A x v²), la portance (L = 1/2 x C_L x ρ x A x v²) et le poids (P = m x g), où C_D et C_L sont les constantes de traînée et de portance, ρ la densité de l'air et A l'aire de la cape.

Détermination de la vitesse et l'accélération

Après avoir établi la trajectoire de Batman lorsqu'il saute d'un building, ils ont pu proposer quatre équations quasiment incompréhensibles, soit deux équations pour la traînée et la portance, en fonction de l'axe x et y (horizontal et vertical). Ils ont ainsi pu trouver deux équations de la somme des forces en fonction de x et y. Soit F_x = L x sinθ - D x cosθ et F_y = (m x g) - L x cosθ - D x sinθ. D'accord, si vous le dites ! Ils sont ensuite passés aux calculs des accélérations en fonction de x et y en utilisant tout simplement les formules a = F/m et cos²θ + sin²θ = 1. On vous évite bien évidemment les calculs, mais de notre coté nous avons vérifié et tout tombe juste ! Je tiens à vous dire qu'on s'est bien cassé la tête pour comprendre comment ils sont passés des équations des sommes des forces aux équations des accélérations ! Mais, après quelques recherches nous avons retrouvé la fameuse formule a = F/m. Heureusement pour nous !

Une vitesse de chute trop élevée

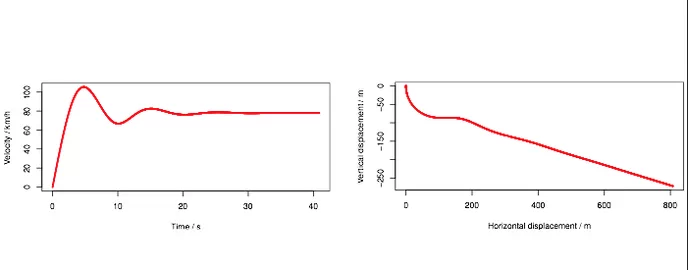
Après avoir déduit que l'aire de la cape de Batman dans Batman Begins est de 2,20 m², que la masse volumique de l'air est de 1,2 km.m³, que le poids de Batman est de 95 kg et que les constantes C_D et C_L sont respectivement égales à 0,4 et 1,45, ils en ont déduit la vitesse de Batman à différentes étapes de sa chute. Après avoir atteint une vitesse maximale de 110 km/h au début de son saut, il va arriver à se stabiliser à 80 km/h sur une distance d'environ 350 mètres. En gros, l'atterrissage au sol va se faire à environ 80 km/h, ce qui semble impensable. Même en augmentant la constante de portance, la vitesse ne réduira pas suffisamment ! Ça va faire très mal.

Ils estiment donc que Batman est capable de voler ou de planer, mais pas d'atterrir sans subir de dommages corporels, même avec une combinaison solide. Bien évidemment, cette étude reste théorique et ne prend pas en considération tous les problèmes technologiques rencontrés dans le film. Ils supposent en effet que le matériau de la cape reste rigide pour permettre à Batman de planer dans les airs, mais peut-être que cette dernière peut s'incliner pour ralentir la chute.

Que faudrait-il à Batman pour atterrir sans problème ?

Mais alors, que faudrait-il ajouter au costume de Batman pour qu'il évite de se tuer à chaque fois qu'il saute d'un gratte-ciel ? D'une part, on pourrait lui dire de sauter d'un gratte-ciel moins haut, ce serait le plus logique. Mais bon, je suis sûr qu'il ne nous écouterait pas et qu'il n'en ferait qu'à sa tête comme à son habitude. Autrement dit, on pourrait demander à Alfred de modifier son costume en y ajoutant une cape plus longue (enfin, avec une surface plus importante). En effet, plus sa cape sera longue, plus il pourra subir la traînée, ce qui lui permettra de réduire sa vitesse de chute.

On pourrait également penser à un parachute que Batman ouvrirait lorsqu'il s'approcherait du point d'impact. C'est vrai, c'est beaucoup moins classe, mais au moins il survivrait à ses chutes vertigineuses. Pourquoi ne pas intégrer un jet pack à son costume. C'est beaucoup plus badass et plus efficace qu'un simple parachute.

Verdict

Comme nous avons pu le voir tout au long de ce Geekbusters, Batman est effectivement capable de planer sur une distance d'environ 350 mètres en sautant d'un gratte-ciel de 150 mètres de haut. Avec une vitesse de croisière d'environ 80 km/h, malheureusement, la science ne donne pas cher de sa peau lorsqu'il effectuera son atterrissage. Il serait donc intéressant d'effectuer quelques modifications à son costume pour réduire sa vitesse de chute et donc sa vitesse à l'impact au sol !